Outline:

Learning weights

  • We’ll need to learn the weights from example data, then use those weights to make the predictions.
  • We want the network to make predictions as close as possible to the real values.
  • To measure this, we need a metric of how wrong the predictions are, the error.

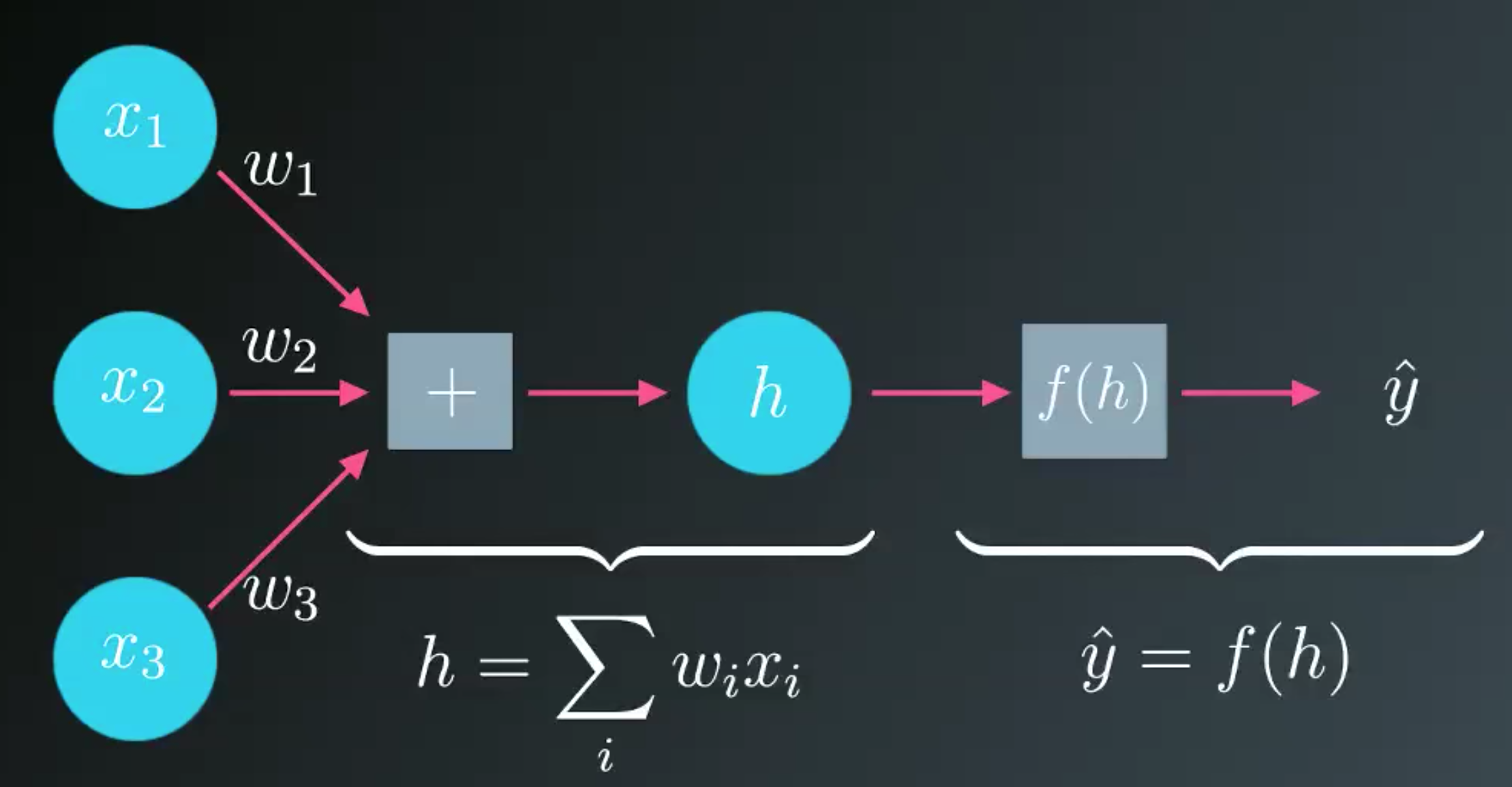
network

Error function

A common metric is the sum of the squared errors (SSE):

sse

  • We want the network’s prediction error to be as small as possible and the weights are the knobs we can use to make that happen.
  • Our goal is to find weights that minimize the squared error .
  • To do this with a neural network, typically you’d use gradient descent.

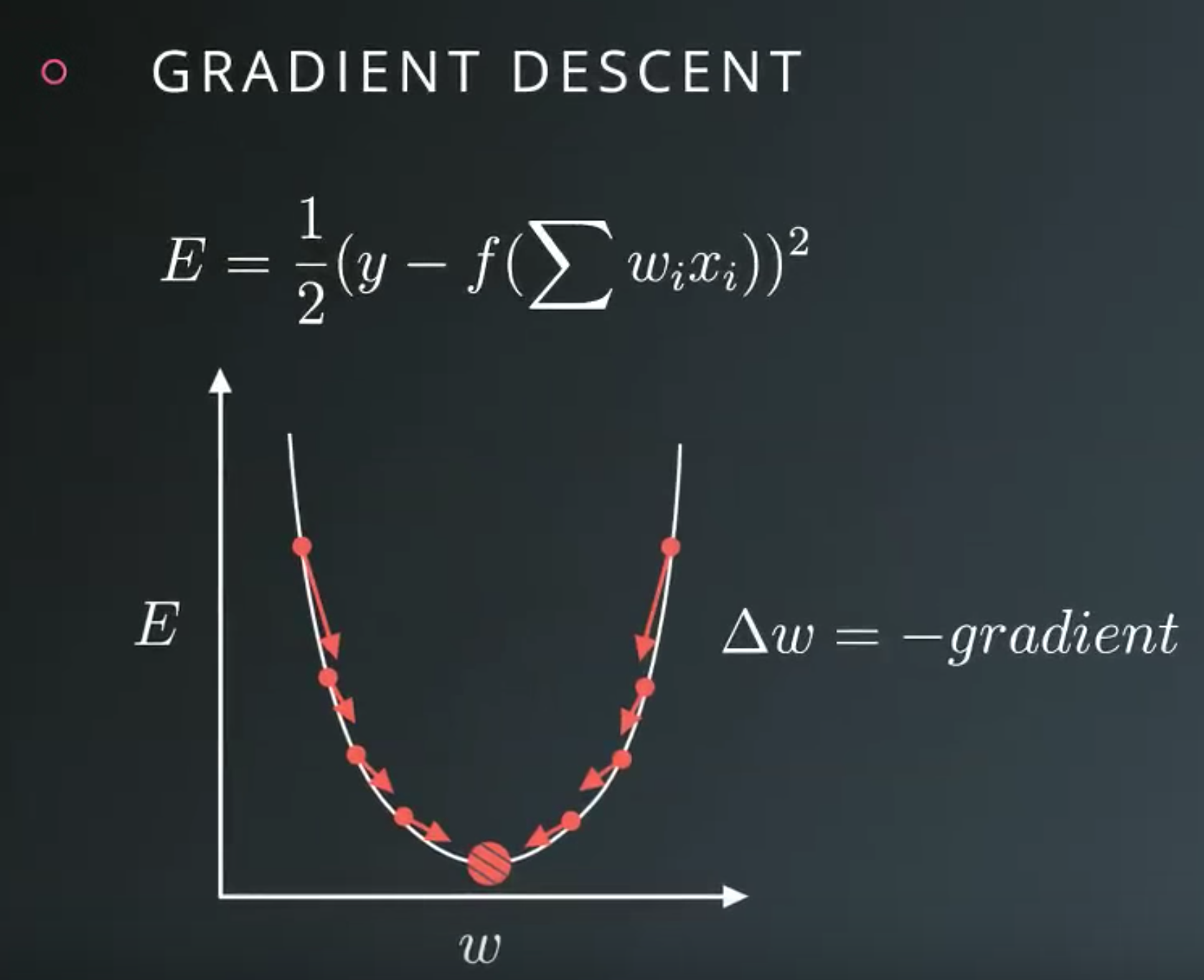
Gradient Descent

  • With gradient descent, we take multiple small steps towards our goal.
  • We want to change the weights in steps that reduce the error.
  • The gradient is just a derivative generalized to functions with more than one variable.
  • We can use calculus to find the gradient at any point in our error function, which depends on the input weights.

gradient

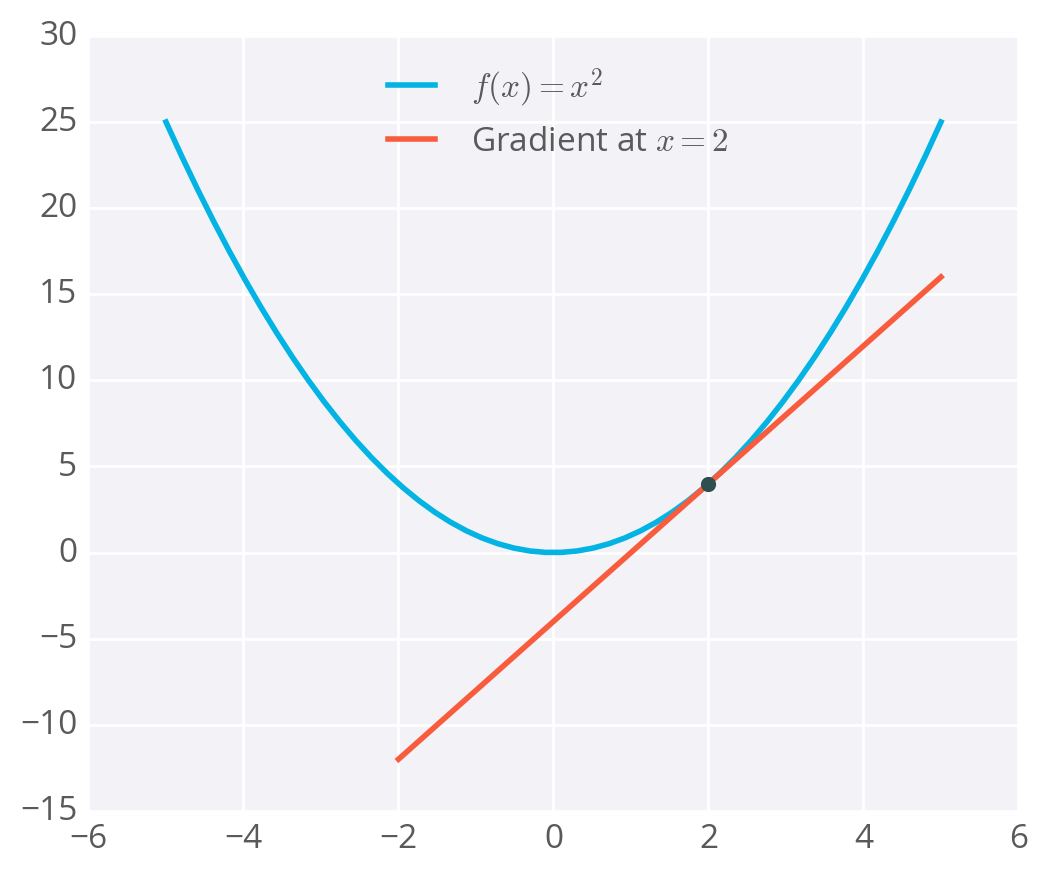
Derivative example

  • The derivative of is .
  • So, at , the slope is .
  • Plotting this out, it looks like:

derivative-example

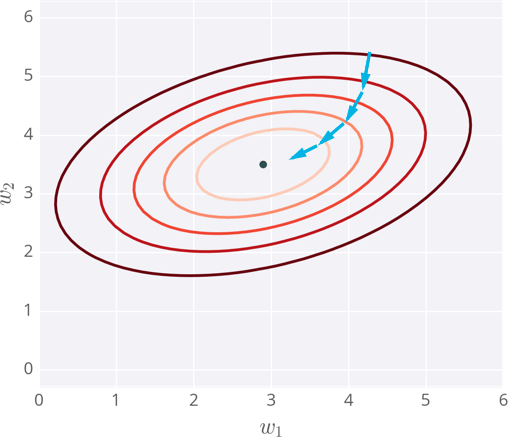
Contour Map

  • Example of the error of a neural network with two inputs, and accordingly, two weights.
  • At each step, you calculate the error and the gradient.
  • Then use those to determine how much to change each weight.
  • Repeating this process will eventually find weights that are close to the minimum of the error function, the block dot in the middle.

gradient-descent

Gradient Descent Math

Learning Rate

learning-rate

Chain Rule

chain-rule

Derivative

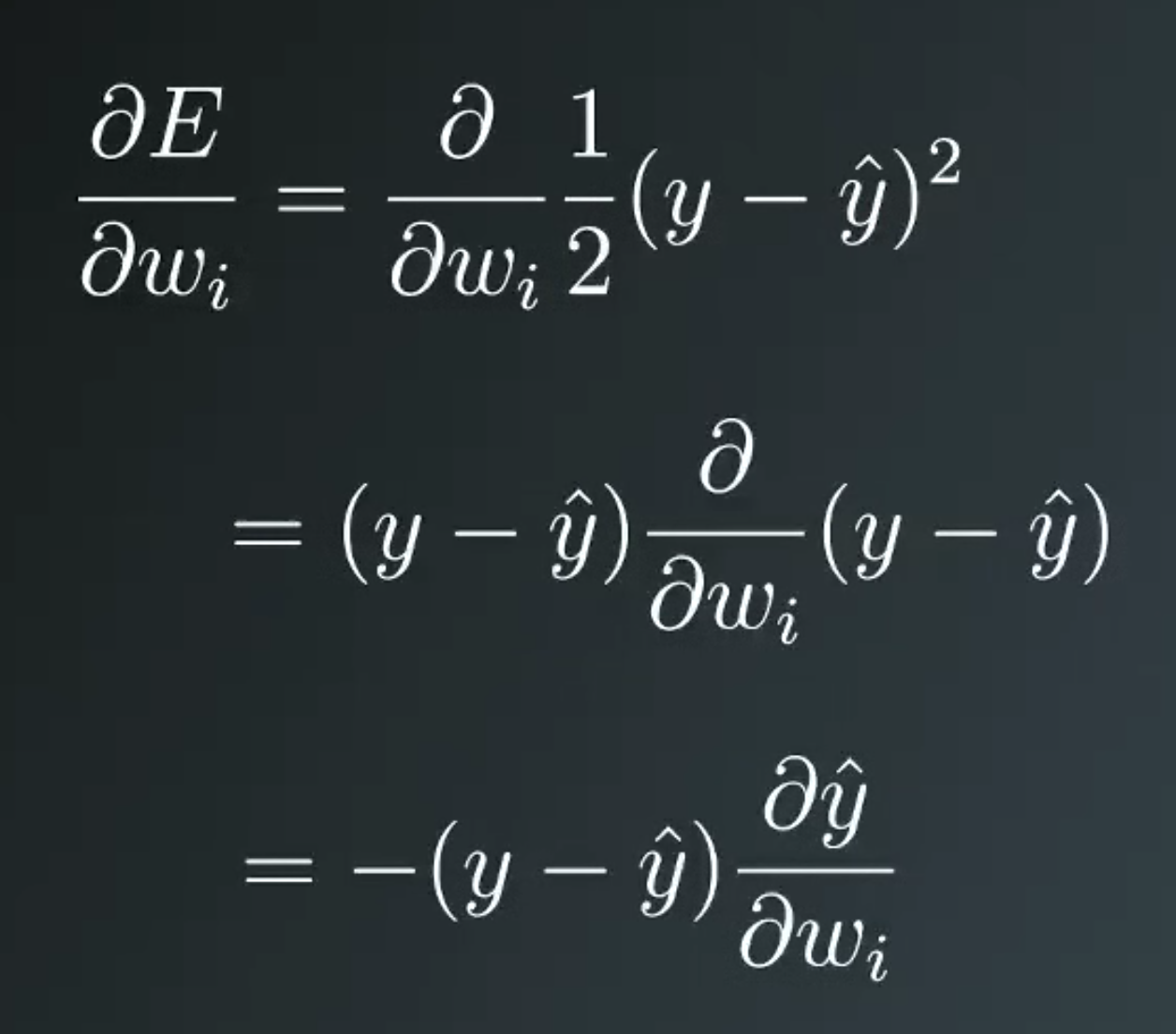
calculation-1

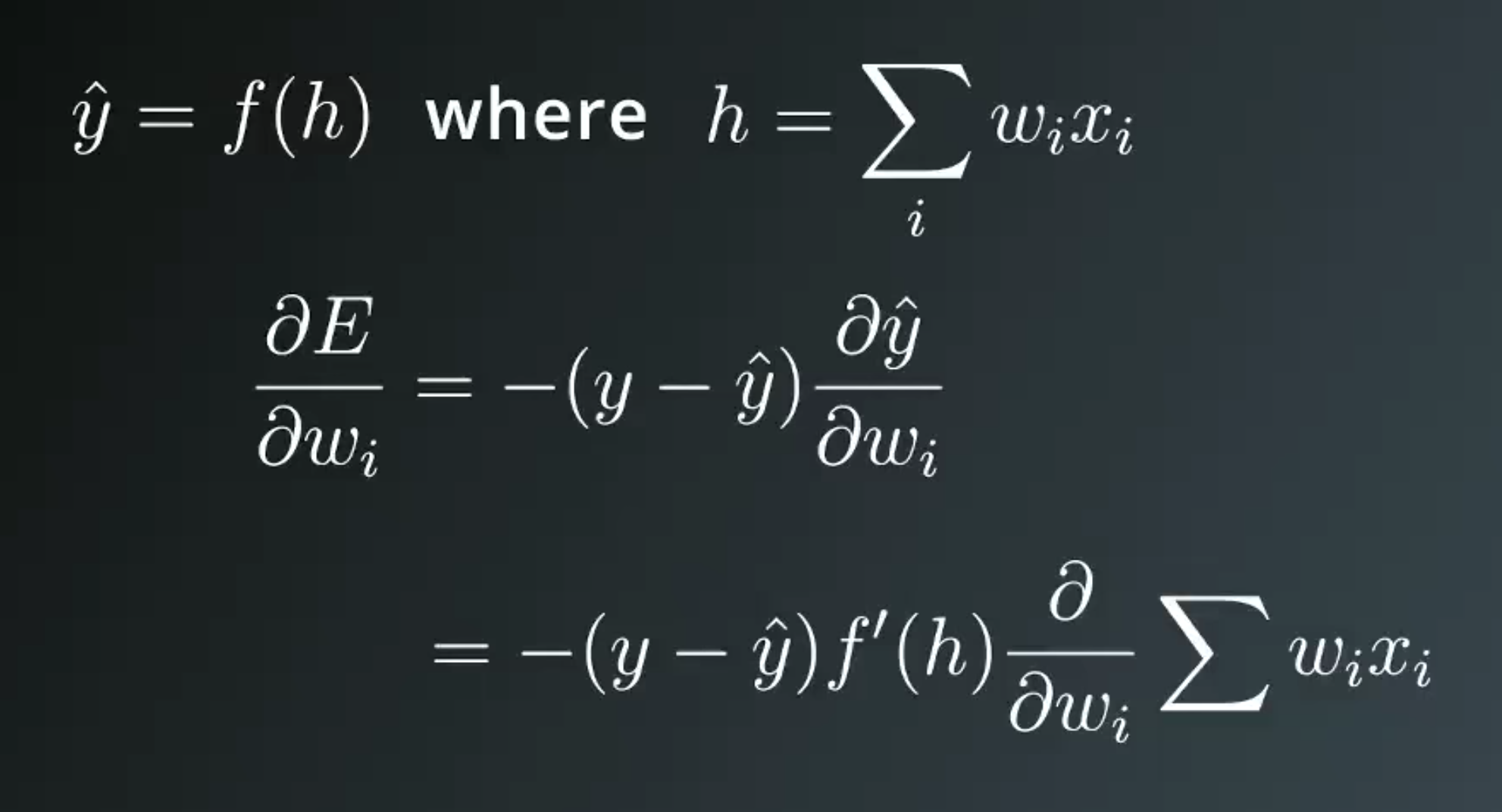
calculation-2

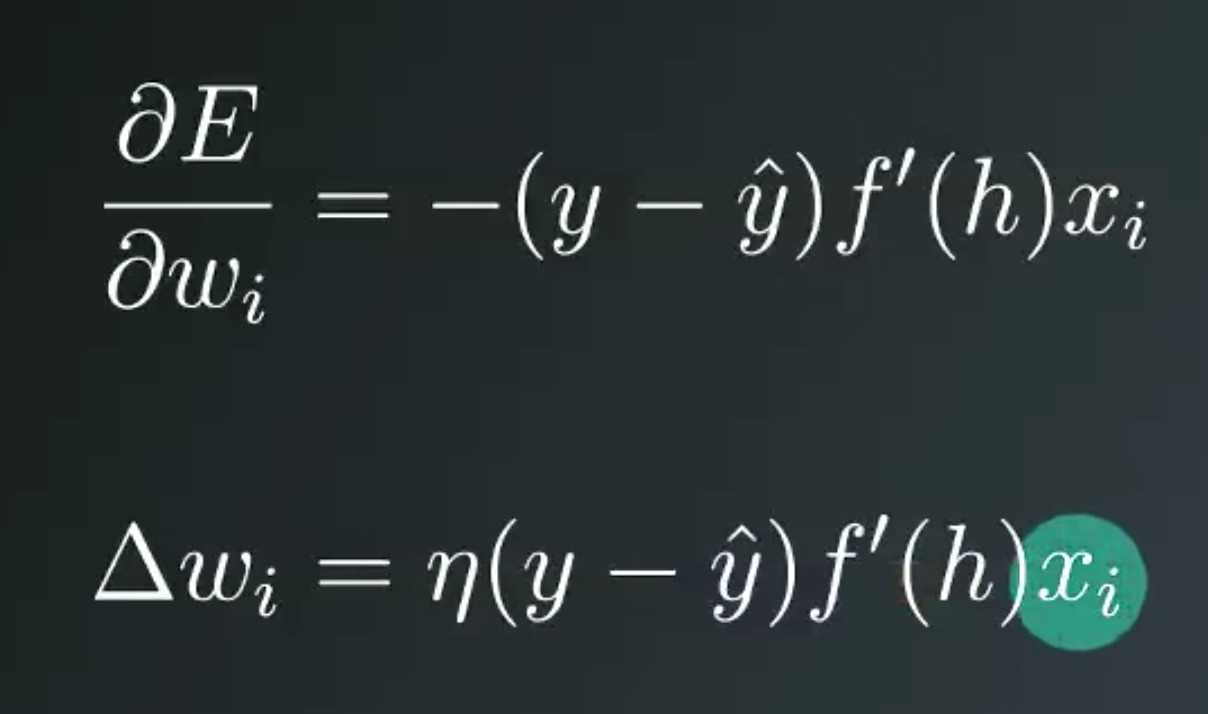
calculation-3

Define error term

calculation-4

Multiple Outpus

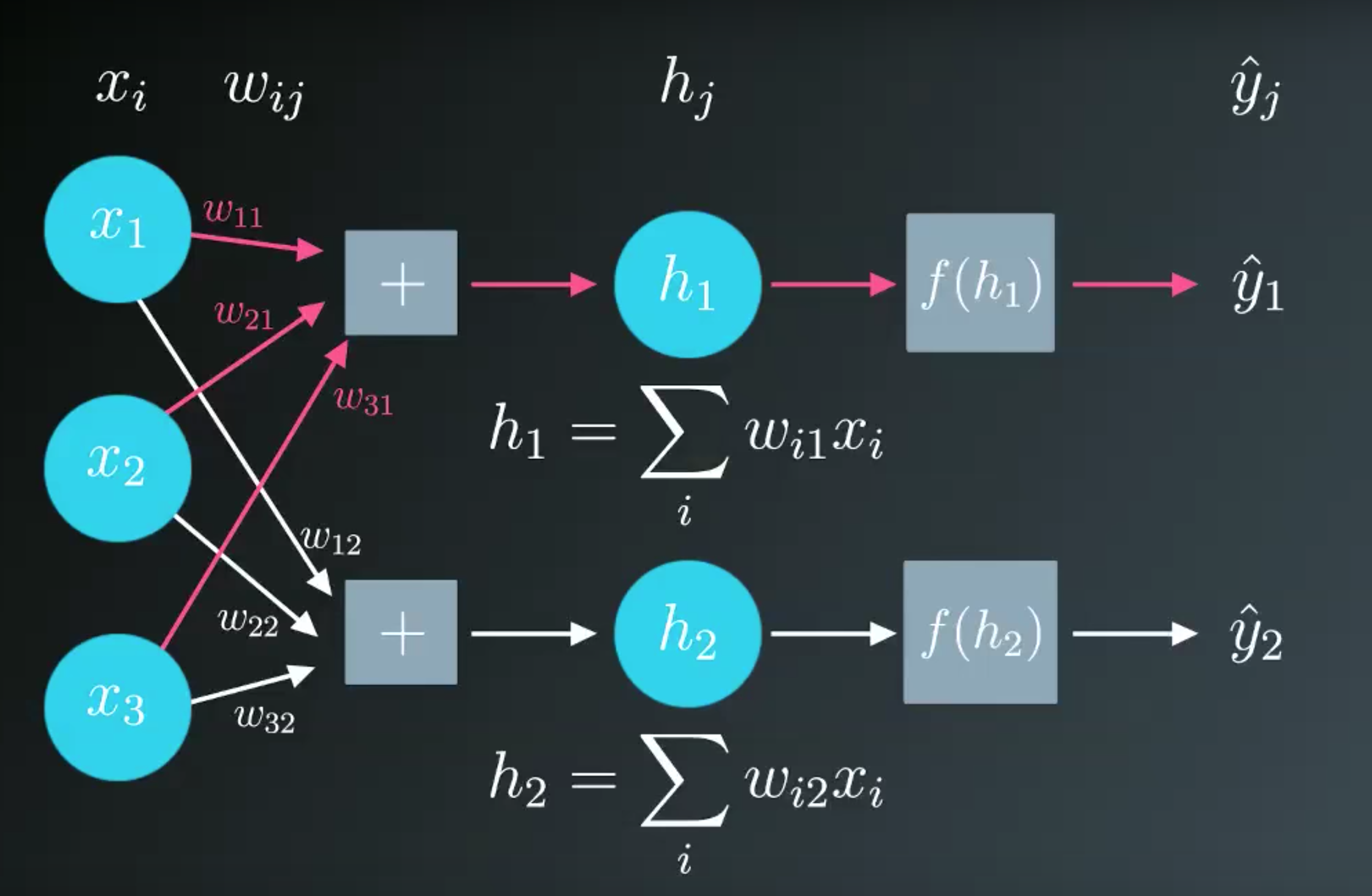
calculation-5

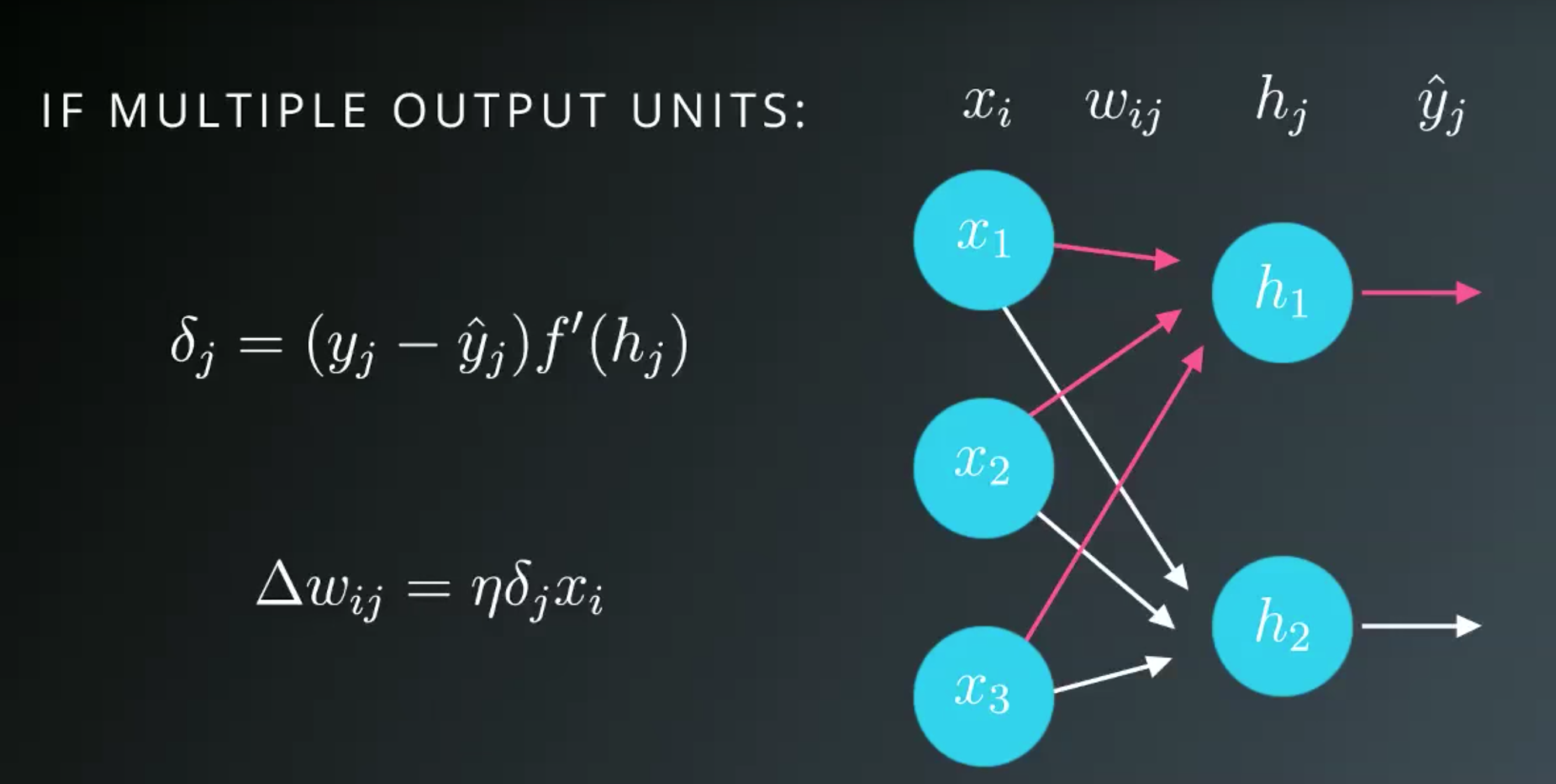
calculation-6

Gradient Descent Code

  • This code is for the case of only one output unit.
  • We’ll also be using the sigmoid as the activation function

Code:

import numpy as np

def sigmoid(x):
    """
    Calculate sigmoid
    """
    return 1/(1+np.exp(-x))

def sigmoid_prime(x):
    """
    # Derivative of the sigmoid function
    """
    return sigmoid(x) * (1 - sigmoid(x))

learnrate = 0.5
x = np.array([1, 2, 3, 4])
y = np.array(0.5)

# Initial weights
w = np.array([0.5, -0.5, 0.3, 0.1])

### Calculate one gradient descent step for each weight
### Note: Some steps have been consilated, so there are
###       fewer variable names than in the above sample code

# TODO: Calculate the node's linear combination of inputs and weights
h = np.dot(x, w)

# TODO: Calculate output of neural network
nn_output = sigmoid(h)

# TODO: Calculate error of neural network
error = y - nn_output

# TODO: Calculate the error term
#       Remember, this requires the output gradient, which we haven't
#       specifically added a variable for.
error_term = error * sigmoid_prime(h)

# TODO: Calculate change in weights
del_w = learnrate * error_term * x

print('Neural Network output:')
print(nn_output)
print('Amount of Error:')
print(error)
print('Change in Weights:')
print(del_w)

Output:

Neural Network output:
0.689974481128
Amount of Error:
-0.189974481128
Change in Weights:
[-0.02031869 -0.04063738 -0.06095608 -0.08127477]

Gradient Descent Implementation

How do we translate that code to calculate many weight updates so our network will learn?

Example Scene

  • Use gradient descent to train a network on graduate school admissions data
  • This dataset has three input features:
    • GRE score
    • GPA
    • Rank of the undergraduate school (numbered 1 through 4)
      • Institutions with rank 1 have the highest prestige, those with rank 4 have the lowest.
  • The goal here is to predict if a student will be admitted to a graduates program based on these features.
  • Network with one output layer with one unit.
  • Sigmoid function for the output unit activation.

Data Cleanup

  • The rank feature is categorical.
  • To standardize the GRE and GPA data
    • to scale the values such they have zero mean and a standard deviation of 1.

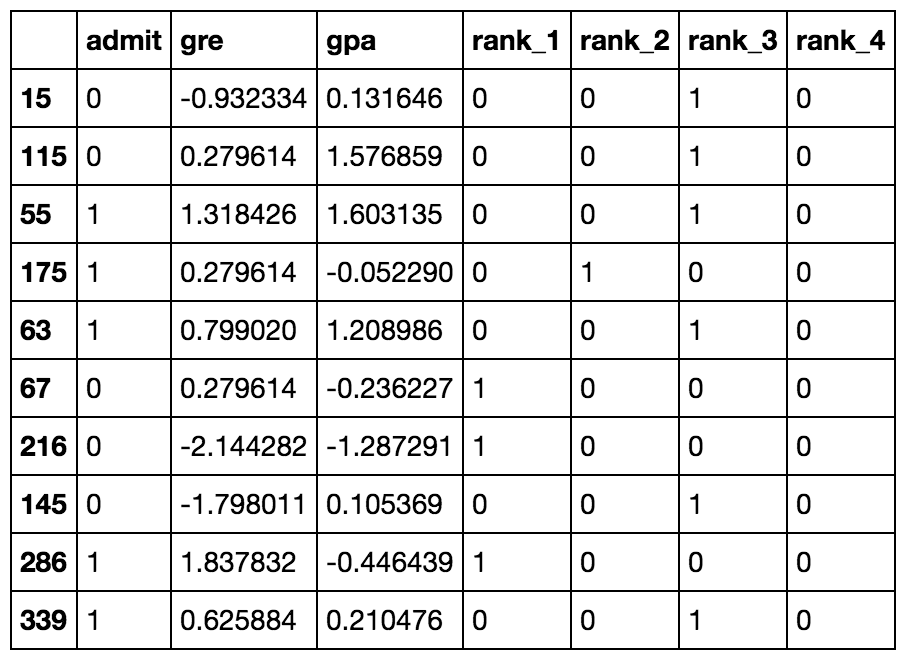
example-data

data_prep.py:

import numpy as np
import pandas as pd

admissions = pd.read_csv('binary.csv')

# Make dummy variables for rank
data = pd.concat([admissions, pd.get_dummies(admissions['rank'], prefix='rank')], axis=1)
data = data.drop('rank', axis=1)

# Standarize features
for field in ['gre', 'gpa']:
    mean, std = data[field].mean(), data[field].std()
    data.loc[:,field] = (data[field]-mean)/std
    
# Split off random 10% of the data for testing
np.random.seed(42)
sample = np.random.choice(data.index, size=int(len(data)*0.9), replace=False)
data, test_data = data.ix[sample], data.drop(sample)

# Split into features and targets
features, targets = data.drop('admit', axis=1), data['admit']
features_test, targets_test = test_data.drop('admit', axis=1), test_data['admit']

Implementation

Code:

import numpy as np
from data_prep import features, targets, features_test, targets_test


def sigmoid(x):
    """
    Calculate sigmoid
    """
    return 1 / (1 + np.exp(-x))

# TODO: We haven't provided the sigmoid_prime function like we did in
#       the previous lesson to encourage you to come up with a more
#       efficient solution. If you need a hint, check out the comments
#       in solution.py from the previous lecture.

# Use to same seed to make debugging easier
np.random.seed(42)

n_records, n_features = features.shape
last_loss = None

# Initialize weights
weights = np.random.normal(scale=1 / n_features**.5, size=n_features)

# Neural Network hyperparameters
epochs = 1000
learnrate = 0.5

for e in range(epochs):
    del_w = np.zeros(weights.shape)
    for x, y in zip(features.values, targets):
        # Loop through all records, x is the input, y is the target

        # Activation of the output unit
        #   Notice we multiply the inputs and the weights here 
        #   rather than storing h as a separate variable 
        output = sigmoid(np.dot(x, weights))

        # The error, the target minus the network output
        error = y - output

        # The error term
        #   Notice we calulate f'(h) here instead of defining a separate
        #   sigmoid_prime function. This just makes it faster because we
        #   can re-use the result of the sigmoid function stored in
        #   the output variable
        error_term = error * output * (1 - output)

        # The gradient descent step, the error times the gradient times the inputs
        del_w += error_term * x

    # Update the weights here. The learning rate times the 
    # change in weights, divided by the number of records to average
    weights += learnrate * del_w / n_records

    # Printing out the mean square error on the training set
    if e % (epochs / 10) == 0:
        out = sigmoid(np.dot(features, weights))
        loss = np.mean((out - targets) ** 2)
        if last_loss and last_loss < loss:
            print("Train loss: ", loss, "  WARNING - Loss Increasing")
        else:
            print("Train loss: ", loss)
        last_loss = loss


# Calculate accuracy on test data
tes_out = sigmoid(np.dot(features_test, weights))
predictions = tes_out > 0.5
accuracy = np.mean(predictions == targets_test)
print("Prediction accuracy: {:.3f}".format(accuracy))

Output:

Train loss:  0.26276093849966364
Train loss:  0.20928619409324895
Train loss:  0.20084292908073417
Train loss:  0.19862156475527884
Train loss:  0.19779851396686018
Train loss:  0.19742577912189863
Train loss:  0.19723507746241065
Train loss:  0.19712945625092465
Train loss:  0.19706766341315074
Train loss:  0.19703005801777368
Prediction accuracy: 0.725

Reference