MiniFlow
Outline:
What is a Neural Network
- A neural network is a graph of mathematical functions:
- linear combinations and activation functions.
- The graph consists of nodes, and edges.
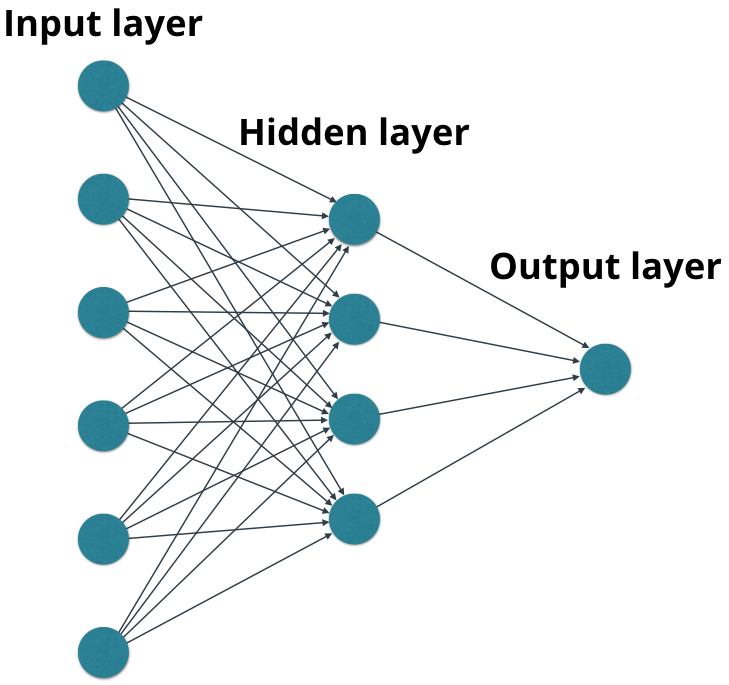
- Nodes in each layer (except for nodes in the input layer) perform mathematical functions using inputs from nodes in the previous layers.
- For example, a node could represent , where and are input values from nodes in the previous layer.
- Each node creates an output value which may be passed to nodes in the next layer.
- The output value from the output layer does not get passed to a future layer (last layer!)
- Layers between the input layer and the output layer are called hidden layers.
- The edges in the graph describe the connections between the nodes, along which the values flow from one layer to the next.
- These edges can also apply operations to the values that flow along them, such as multiplying by weights, adding biases, etc..
Graphs
- The nodes and edges create a graph structure.
- It isn’t hard to imagine that increasingly complex graphs can calculate almost anything.
- There are generally two steps to create neural networks:
- Define the graph of nodes and edges.
- Propagate values through the graph.
Gradient Descent
- Technically, the gradient actually points uphill, in the direction of steepest ascent.
- But if we put a
-sign in front of this value, we get the direction of steepest descent, which is what we want. - How much force should be applied to the push. This is known as the learning rate.
- which is an apt name since this value determines how quickly or slowly the neural network learns.
- This is more of a guessing game than anything else but empirically values in the range 0.1 to 0.0001 work well.
- The range 0.001 to 0.0001 is popular, as 0.1 and 0.01 are sometimes too large.
Gradient-Descent-Convergence:

Gradient-Descent-Civergence:

Code:
"""
Given the starting point of any `x` gradient descent
should be able to find the minimum value of x for the
cost function `f` defined below.
"""
import random
from gd import gradient_descent_update
def f(x):
"""
Quadratic function.
It's easy to see the minimum value of the function
is 5 when is x=0.
"""
return x**2 + 5
def df(x):
"""
Derivative of `f` with respect to `x`.
"""
return 2*x
def gradient_descent_update(x, gradx, learning_rate):
"""
Performs a gradient descent update.
"""
# TODO: Implement gradient descent.
# Return the new value for x
return x - learning_rate * gradx
# Random number between 0 and 10,000. Feel free to set x whatever you like.
x = random.randint(0, 10000)
# TODO: Set the learning rate
learning_rate = 0.1
epochs = 100
for i in range(epochs+1):
cost = f(x)
gradx = df(x)
print("EPOCH {}: Cost = {:.3f}, x = {:.3f}".format(i, cost, gradx))
x = gradient_descent_update(x, gradx, learning_rate)
Output:
EPOCH 0: Cost = 2601774.000, x = 3226.000
EPOCH 1: Cost = 1665137.160, x = 2580.800
EPOCH 2: Cost = 1065689.582, x = 2064.640
EPOCH 3: Cost = 682043.133, x = 1651.712
EPOCH 4: Cost = 436509.405, x = 1321.370
EPOCH 5: Cost = 279367.819, x = 1057.096
EPOCH 6: Cost = 178797.204, x = 845.677
EPOCH 7: Cost = 114432.011, x = 676.541
EPOCH 8: Cost = 73238.287, x = 541.233
EPOCH 9: Cost = 46874.304, x = 432.986
EPOCH 10: Cost = 30001.354, x = 346.389
EPOCH 11: Cost = 19202.667, x = 277.111
EPOCH 12: Cost = 12291.507, x = 221.689
EPOCH 13: Cost = 7868.364, x = 177.351
EPOCH 14: Cost = 5037.553, x = 141.881
EPOCH 15: Cost = 3225.834, x = 113.505
EPOCH 16: Cost = 2066.334, x = 90.804
EPOCH 17: Cost = 1324.254, x = 72.643
EPOCH 18: Cost = 849.322, x = 58.114
EPOCH 19: Cost = 545.366, x = 46.492
EPOCH 20: Cost = 350.834, x = 37.193
EPOCH 21: Cost = 226.334, x = 29.755
EPOCH 22: Cost = 146.654, x = 23.804
EPOCH 23: Cost = 95.658, x = 19.043
EPOCH 24: Cost = 63.021, x = 15.234
EPOCH 25: Cost = 42.134, x = 12.187
EPOCH 26: Cost = 28.766, x = 9.750
EPOCH 27: Cost = 20.210, x = 7.800
EPOCH 28: Cost = 14.734, x = 6.240
EPOCH 29: Cost = 11.230, x = 4.992
EPOCH 30: Cost = 8.987, x = 3.994
EPOCH 31: Cost = 7.552, x = 3.195
EPOCH 32: Cost = 6.633, x = 2.556
EPOCH 33: Cost = 6.045, x = 2.045
EPOCH 34: Cost = 5.669, x = 1.636
EPOCH 35: Cost = 5.428, x = 1.309
EPOCH 36: Cost = 5.274, x = 1.047
EPOCH 37: Cost = 5.175, x = 0.838
EPOCH 38: Cost = 5.112, x = 0.670
EPOCH 39: Cost = 5.072, x = 0.536
EPOCH 40: Cost = 5.046, x = 0.429
Stochastic Gradient Descent
- Stochastic Gradient Descent (SGD) is a version of Gradient Descent
- Where on each forward pass a batch of data is randomly sampled from total dataset.
- Ideally, the entire dataset would be fed into the neural network on each forward pass.
- But in practice, it’s not practical due to memory constraints.
- SGD is an approximation of Gradient Descent.
- The more batches processed by the neural network, the better the approximation.
A naïve implementation of SGD involves:
- Randomly sample a batch of data from the total dataset.
- Running the network forward and backward to calculate the gradient (with data from (1)).
- Apply the gradient descent update.
- Repeat steps 1-3 until convergence or the loop is stopped by another mechanism (i.e. the number of epochs).
Code: miniflow.py
import numpy as np
class Node:
"""
Base class for nodes in the network.
Arguments:
`inbound_nodes`: A list of nodes with edges into this node.
"""
def __init__(self, inbound_nodes=[]):
"""
Node's constructor (runs when the object is instantiated). Sets
properties that all nodes need.
"""
# A list of nodes with edges into this node.
self.inbound_nodes = inbound_nodes
# The eventual value of this node. Set by running
# the forward() method.
self.value = None
# A list of nodes that this node outputs to.
self.outbound_nodes = []
# New property! Keys are the inputs to this node and
# their values are the partials of this node with
# respect to that input.
self.gradients = {}
# Sets this node as an outbound node for all of
# this node's inputs.
for node in inbound_nodes:
node.outbound_nodes.append(self)
def forward(self):
"""
Every node that uses this class as a base class will
need to define its own `forward` method.
"""
raise NotImplementedError
def backward(self):
"""
Every node that uses this class as a base class will
need to define its own `backward` method.
"""
raise NotImplementedError
class Input(Node):
"""
A generic input into the network.
"""
def __init__(self):
# The base class constructor has to run to set all
# the properties here.
#
# The most important property on an Input is value.
# self.value is set during `topological_sort` later.
Node.__init__(self)
def forward(self):
# Do nothing because nothing is calculated.
pass
def backward(self):
# An Input node has no inputs so the gradient (derivative)
# is zero.
# The key, `self`, is reference to this object.
self.gradients = {self: 0}
# Weights and bias may be inputs, so you need to sum
# the gradient from output gradients.
for n in self.outbound_nodes:
self.gradients[self] += n.gradients[self]
class Linear(Node):
"""
Represents a node that performs a linear transform.
"""
def __init__(self, X, W, b):
# The base class (Node) constructor. Weights and bias
# are treated like inbound nodes.
Node.__init__(self, [X, W, b])
def forward(self):
"""
Performs the math behind a linear transform.
"""
X = self.inbound_nodes[0].value
W = self.inbound_nodes[1].value
b = self.inbound_nodes[2].value
self.value = np.dot(X, W) + b
def backward(self):
"""
Calculates the gradient based on the output values.
"""
# Initialize a partial for each of the inbound_nodes.
self.gradients = {n: np.zeros_like(n.value) for n in self.inbound_nodes}
# Cycle through the outputs. The gradient will change depending
# on each output, so the gradients are summed over all outputs.
for n in self.outbound_nodes:
# Get the partial of the cost with respect to this node.
grad_cost = n.gradients[self]
# Set the partial of the loss with respect to this node's inputs.
self.gradients[self.inbound_nodes[0]] += np.dot(grad_cost, self.inbound_nodes[1].value.T)
# Set the partial of the loss with respect to this node's weights.
self.gradients[self.inbound_nodes[1]] += np.dot(self.inbound_nodes[0].value.T, grad_cost)
# Set the partial of the loss with respect to this node's bias.
self.gradients[self.inbound_nodes[2]] += np.sum(grad_cost, axis=0, keepdims=False)
class Sigmoid(Node):
"""
Represents a node that performs the sigmoid activation function.
"""
def __init__(self, node):
# The base class constructor.
Node.__init__(self, [node])
def _sigmoid(self, x):
"""
This method is separate from `forward` because it
will be used with `backward` as well.
`x`: A numpy array-like object.
"""
return 1. / (1. + np.exp(-x))
def forward(self):
"""
Perform the sigmoid function and set the value.
"""
input_value = self.inbound_nodes[0].value
self.value = self._sigmoid(input_value)
def backward(self):
"""
Calculates the gradient using the derivative of
the sigmoid function.
"""
# Initialize the gradients to 0.
self.gradients = {n: np.zeros_like(n.value) for n in self.inbound_nodes}
# Sum the partial with respect to the input over all the outputs.
for n in self.outbound_nodes:
grad_cost = n.gradients[self]
sigmoid = self.value
self.gradients[self.inbound_nodes[0]] += sigmoid * (1 - sigmoid) * grad_cost
class MSE(Node):
def __init__(self, y, a):
"""
The mean squared error cost function.
Should be used as the last node for a network.
"""
# Call the base class' constructor.
Node.__init__(self, [y, a])
def forward(self):
"""
Calculates the mean squared error.
"""
# NOTE: We reshape these to avoid possible matrix/vector broadcast
# errors.
#
# For example, if we subtract an array of shape (3,) from an array of shape
# (3,1) we get an array of shape(3,3) as the result when we want
# an array of shape (3,1) instead.
#
# Making both arrays (3,1) insures the result is (3,1) and does
# an elementwise subtraction as expected.
y = self.inbound_nodes[0].value.reshape(-1, 1)
a = self.inbound_nodes[1].value.reshape(-1, 1)
self.m = self.inbound_nodes[0].value.shape[0]
# Save the computed output for backward.
self.diff = y - a
self.value = np.mean(self.diff**2)
def backward(self):
"""
Calculates the gradient of the cost.
"""
self.gradients[self.inbound_nodes[0]] = (2 / self.m) * self.diff
self.gradients[self.inbound_nodes[1]] = (-2 / self.m) * self.diff
def topological_sort(feed_dict):
"""
Sort the nodes in topological order using Kahn's Algorithm.
`feed_dict`: A dictionary where the key is a `Input` Node and the value is the respective value feed to that Node.
Returns a list of sorted nodes.
"""
input_nodes = [n for n in feed_dict.keys()]
G = {}
nodes = [n for n in input_nodes]
while len(nodes) > 0:
n = nodes.pop(0)
if n not in G:
G[n] = {'in': set(), 'out': set()}
for m in n.outbound_nodes:
if m not in G:
G[m] = {'in': set(), 'out': set()}
G[n]['out'].add(m)
G[m]['in'].add(n)
nodes.append(m)
L = []
S = set(input_nodes)
while len(S) > 0:
n = S.pop()
if isinstance(n, Input):
n.value = feed_dict[n]
L.append(n)
for m in n.outbound_nodes:
G[n]['out'].remove(m)
G[m]['in'].remove(n)
# if no other incoming edges add to S
if len(G[m]['in']) == 0:
S.add(m)
return L
def forward_and_backward(graph):
"""
Performs a forward pass and a backward pass through a list of sorted Nodes.
Arguments:
`graph`: The result of calling `topological_sort`.
"""
# Forward pass
for n in graph:
n.forward()
# Backward pass
# see: https://docs.python.org/2.3/whatsnew/section-slices.html
for n in graph[::-1]:
n.backward()
def sgd_update(trainables, learning_rate=1e-2):
"""
Updates the value of each trainable with SGD.
Arguments:
`trainables`: A list of `Input` Nodes representing weights/biases.
`learning_rate`: The learning rate.
"""
# Performs SGD
#
# Loop over the trainables
for t in trainables:
# Change the trainable's value by subtracting the learning rate
# multiplied by the partial of the cost with respect to this
# trainable.
partial = t.gradients[t]
t.value -= learning_rate * partial
Code: nn.py
"""
Have fun with the number of epochs!
Be warned that if you increase them too much,
the VM will time out :)
"""
import numpy as np
from sklearn.datasets import load_boston
from sklearn.utils import shuffle, resample
from miniflow import *
# Load data
data = load_boston()
X_ = data['data']
y_ = data['target']
# Normalize data
X_ = (X_ - np.mean(X_, axis=0)) / np.std(X_, axis=0)
n_features = X_.shape[1]
n_hidden = 10
W1_ = np.random.randn(n_features, n_hidden)
b1_ = np.zeros(n_hidden)
W2_ = np.random.randn(n_hidden, 1)
b2_ = np.zeros(1)
# Neural network
X, y = Input(), Input()
W1, b1 = Input(), Input()
W2, b2 = Input(), Input()
l1 = Linear(X, W1, b1)
s1 = Sigmoid(l1)
l2 = Linear(s1, W2, b2)
cost = MSE(y, l2)
feed_dict = {
X: X_,
y: y_,
W1: W1_,
b1: b1_,
W2: W2_,
b2: b2_
}
epochs = 10
# Total number of examples
m = X_.shape[0]
batch_size = 11
steps_per_epoch = m // batch_size
graph = topological_sort(feed_dict)
trainables = [W1, b1, W2, b2]
print("Total number of examples = {}".format(m))
# Step 4
for i in range(epochs):
loss = 0
for j in range(steps_per_epoch):
# Step 1
# Randomly sample a batch of examples
X_batch, y_batch = resample(X_, y_, n_samples=batch_size)
# Reset value of X and y Inputs
X.value = X_batch
y.value = y_batch
# Step 2
forward_and_backward(graph)
# Step 3
sgd_update(trainables)
loss += graph[-1].value
print("Epoch: {}, Loss: {:.3f}".format(i+1, loss/steps_per_epoch))
Output:
Total number of examples = 506
Epoch: 1, Loss: 137.353
Epoch: 2, Loss: 38.041
Epoch: 3, Loss: 30.666
Epoch: 4, Loss: 24.717
Epoch: 5, Loss: 23.817
...
...
...
Epoch: 994, Loss: 3.993
Epoch: 995, Loss: 3.549
Epoch: 996, Loss: 4.550
Epoch: 997, Loss: 3.830
Epoch: 998, Loss: 3.975
Epoch: 999, Loss: 3.160
Epoch: 1000, Loss: 3.711