Backpropagation

Outline:

• Backpropagation
• Example
• Backpropagation Code
• Implementing Backpropagation

Backpropagation

• How to make a multilayer neural network learn.
• The backpropagation algorithm using the chain rule to find the error with the respect to the weights connecting the input layer to the hidden layer (for a two layer network).

• To update the weights to hidden layers using gradient descent
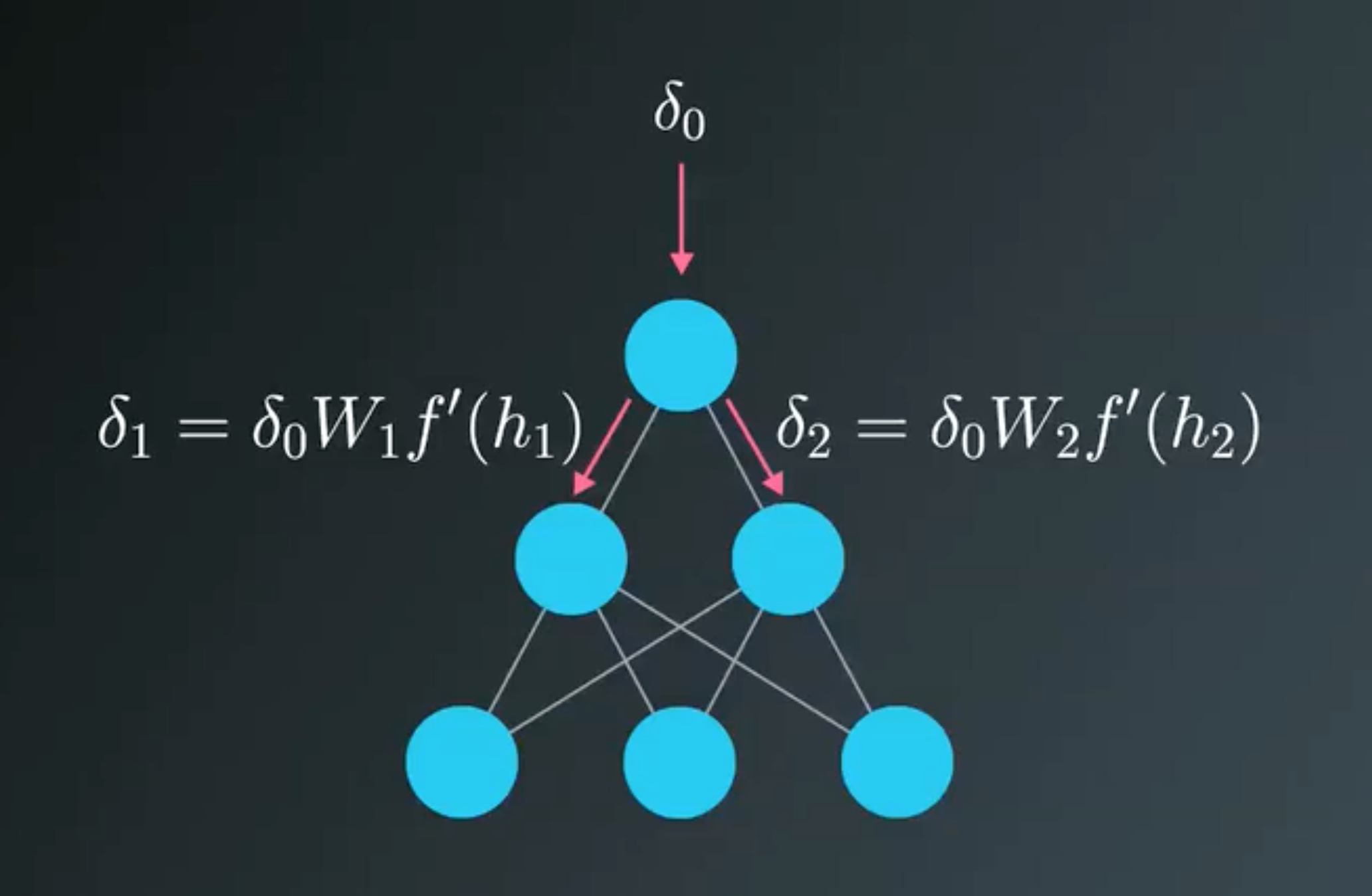
  • How much error each of the hidden units contributed to the final output
  • The output of a layer is determined by the weights between layers, the error resulting from units is scaled by the weights going forward through the network.
  • We know the error at the output, we can use the weights to work backwards to hidden layers.

The error attributed to hidden unit $j$ is the output errors, scaled by the weights between the output and hidden layers (and the gradient):

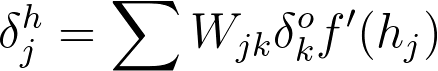
The gradient descent step is the same as before, just with the new errors:

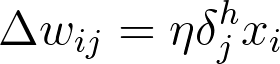
The weight steps are equal to the step size times the output error of the layer times the values of the inputs to that layer

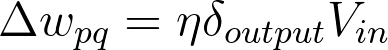
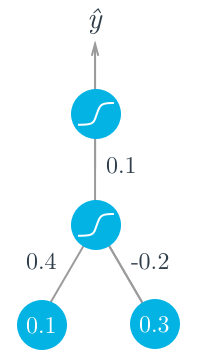
Example

• Two input values, one hidden unit, and one output unit.
• Sigmoid activations on the hidden and output units.

Backpropagation Code

Code:

import numpy as np


def sigmoid(x):
    """
    Calculate sigmoid
    """
    return 1 / (1 + np.exp(-x))


x = np.array([0.5, 0.1, -0.2])
target = 0.6
learnrate = 0.5

weights_input_hidden = np.array([[0.5, -0.6],
                                 [0.1, -0.2],
                                 [0.1, 0.7]])

weights_hidden_output = np.array([0.1, -0.3])

## Forward pass
hidden_layer_input = np.dot(x, weights_input_hidden)
hidden_layer_output = sigmoid(hidden_layer_input)

output_layer_in = np.dot(hidden_layer_output, weights_hidden_output)
output = sigmoid(output_layer_in)

## Backwards pass
## TODO: Calculate output error
error = target - output

# TODO: Calculate error term for output layer
output_error_term = error * output * (1 - output)

# TODO: Calculate error term for hidden layer
hidden_error_term = np.dot(output_error_term, weights_hidden_output) * hidden_layer_output * (1 - hidden_layer_output)

# TODO: Calculate change in weights for hidden layer to output layer
delta_w_h_o = learnrate * output_error_term * hidden_layer_output

# TODO: Calculate change in weights for input layer to hidden layer
delta_w_i_h = learnrate * hidden_error_term * x[:, None]

print('Change in weights for hidden layer to output layer:')
print(delta_w_h_o)
print('Change in weights for input layer to hidden layer:')
print(delta_w_i_h)

Output:

Change in weights for hidden layer to output layer:
[ 0.00804047  0.00555918]
Change in weights for input layer to hidden layer:
[[  1.77005547e-04  -5.11178506e-04]
 [  3.54011093e-05  -1.02235701e-04]
 [ -7.08022187e-05   2.04471402e-04]]

Nice job!  That's right!

Implementing Backpropagation

• The error term for the output layer:

$$\delta_{k} = (y_{k} - \hat{y}) f^{\prime}(a_K)$$

• The error term for the hidden layer:

$$\delta_{j} = \Sigma [w_{ij} \delta_{k}] f^{\prime}(h_{j})$$

• A simple network with one hidden layer and one output unit
  • Data preparation and data is same as the previous example

Code:

import numpy as np
from data_prep import features, targets, features_test, targets_test

np.random.seed(21)

def sigmoid(x):
    """
    Calculate sigmoid
    """
    return 1 / (1 + np.exp(-x))


# Hyperparameters
n_hidden = 2  # number of hidden units
epochs = 900
learnrate = 0.005

n_records, n_features = features.shape
last_loss = None
# Initialize weights
weights_input_hidden = np.random.normal(scale=1 / n_features ** .5,
                                        size=(n_features, n_hidden))
weights_hidden_output = np.random.normal(scale=1 / n_features ** .5,
                                         size=n_hidden)

for e in range(epochs):
    del_w_input_hidden = np.zeros(weights_input_hidden.shape)
    del_w_hidden_output = np.zeros(weights_hidden_output.shape)
    for x, y in zip(features.values, targets):
        ## Forward pass ##
        # TODO: Calculate the output
        hidden_input = np.dot(x, weights_input_hidden)
        hidden_output = sigmoid(hidden_input)

        output = sigmoid(np.dot(hidden_output,
                                weights_hidden_output))

        ## Backward pass ##
        # TODO: Calculate the network's prediction error
        error = y - output

        # TODO: Calculate error term for the output unit
        output_error_term = error * output * (1 - output)

        ## propagate errors to hidden layer

        # TODO: Calculate the hidden layer's contribution to the error
        hidden_error = np.dot(output_error_term, weights_hidden_output)

        # TODO: Calculate the error term for the hidden layer
        hidden_error_term = hidden_error * hidden_output * (1 - hidden_output)

        # TODO: Update the change in weights
        del_w_hidden_output += output_error_term * hidden_output
        del_w_input_hidden += hidden_error_term * x[:, None]

    # TODO: Update weights
    weights_input_hidden += learnrate * del_w_input_hidden / n_records
    weights_hidden_output += learnrate * del_w_hidden_output / n_records

    # Printing out the mean square error on the training set
    if e % (epochs / 10) == 0:
        hidden_output = sigmoid(np.dot(x, weights_input_hidden))
        out = sigmoid(np.dot(hidden_output,
                             weights_hidden_output))
        loss = np.mean((out - targets) ** 2)

        if last_loss and last_loss < loss:
            print("Train loss: ", loss, "  WARNING - Loss Increasing")
        else:
            print("Train loss: ", loss)
        last_loss = loss

# Calculate accuracy on test data
hidden = sigmoid(np.dot(features_test, weights_input_hidden))
out = sigmoid(np.dot(hidden, weights_hidden_output))
predictions = out > 0.5
accuracy = np.mean(predictions == targets_test)
print("Prediction accuracy: {:.3f}".format(accuracy))

Output:

Train loss:  0.251357252426
Train loss:  0.249965407188
Train loss:  0.248620052189
Train loss:  0.247319932172
Train loss:  0.246063804656
Train loss:  0.244850441793
Train loss:  0.243678632019
Train loss:  0.242547181518
Train loss:  0.241454915502
Train loss:  0.240400679325
Prediction accuracy: 0.725